確率ロボティクス第6回: 動く確率分布（その2）

千葉工業大学 上田 隆一


This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Creative Commons License

確率ロボティクス第6回

今回の内容

  • 動く物体と確率
    • 「非線形なロボット」が移動するときの分布の推移、予測

画像: 気象庁 CC BY-SA 4.0

確率ロボティクス第6回

「非線形なロボット」の位置予測

  • つまり普通のロボットの位置予測
確率ロボティクス第6回

「線形」と「非線形」

  • 線形な状態方程式
  • ロボットには向きがあるので↑のようにならない（非線形に）
    • 例: 右の図のようなロボットの場合
      （制御指令は速度と角速度）

        • : との間の（離散でない連続の）時間
確率ロボティクス第6回

非線形な場合の難しさ

  • 再生性がなくなる
    • ロボットが動くと予測の確率分布が非ガウス分布に
  • 右図: 4章の実験を100回繰り返したもの
    • 向きが雑音でずれるほど軸方向の進みが悪く
      バナナ型の分布に

とりあえずいけるところまでを計算してみましょう

確率ロボティクス第6回

ロボットの移動量の計算

  • ロボット座標系での移動量を制御指令とみなして状態方程式をたてましょう
    • は移動前の姿勢が基準
  • 方針
    • 世界座標系での移動量を考える
    • との関係の式をたてる

    • を状態方程式とする

答えは次のページ

確率ロボティクス第6回

ロボットの移動量の計算（答え）

  • 座標の関係は回転行列で表現できる
  • の変化量は両座標系で同じ
  • まとめると
      • ここで
        （同次変換行列）
  • 状態方程式:
確率ロボティクス第6回

非線形性の確認と対策

  • 状態方程式:
  • 線形な式にはならない
    • のなかに中のが紛れ込む
  • （ガウス分布と想定）からを求めるときに、の分布内のの移動が1方向に揃わないのでが歪んでガウス分布にならない
  • どうやってを求めるか？
    • 再生性を使わない（あとで）
    • 線形近似する
確率ロボティクス第6回

線形近似



  • と近似
    • をで代用
      • : の分布の中心位置

      • なので、をの成分で代用
    • : 近似によるズレの補正
      • 中心から離れるほど大きく補正が必要に

をどう求めるか？

確率ロボティクス第6回

の算出

  • 再掲:
  • とはなにか？
    • がからズレたときののズレの割合
      ヤコビ行列
      • 分母がズレに相当
  • とおきましょう
確率ロボティクス第6回

の算出（続き）



    • はの成分
確率ロボティクス第6回

近似式

  • 状態方程式に
    を代入

    • ここで
      • （単なる略記）
確率ロボティクス第6回

線形化された式からの分布の移動の計算

  • 移動前の分布と移動による雑音の分布

  • （前ページ求めた近似式）を次のように分解
    • 、それぞれの分布を考え、あとでの分布を考える（意味は後で）
確率ロボティクス第6回

、の分布

  • いずれも線形変換の式を使って変換
  • の分布

    • はの線形変換


  • の分布
    • はの線形変換
確率ロボティクス第6回

の分布

  • ガウス分布にしたがう2変数の和の分布はガウス分布
  • 共分散行列の意味
    • のばらつき（上図）: 非線形性（の向きが分布内の姿勢で違うこと）による誤差の拡大
    • のばらつき（下図）: 動き自体の雑音
確率ロボティクス第6回

「非線形なロボット」の位置予測のまとめ

  • 線形近似すればガウス分布で分布の移動・変形を計算できる
    • ただし近似
確率ロボティクス第6回

ガウス分布を使わない方法

  • モンテカルロ法
  • ヒストグラムフィルタ
確率ロボティクス第6回

モンテカルロ法

  • こうするとの集団はからサンプリングされたデータに
    • ロボットの分身をたくさん用意
    • それぞれの分身を状態遷移分布を使って動かす
  • 線形化する方法との違い
    • 任意の分布を表現できる
      • とくに状態遷移が分岐する場合（下図）
    • 計算量は行列の計算より大きく
確率ロボティクス第6回

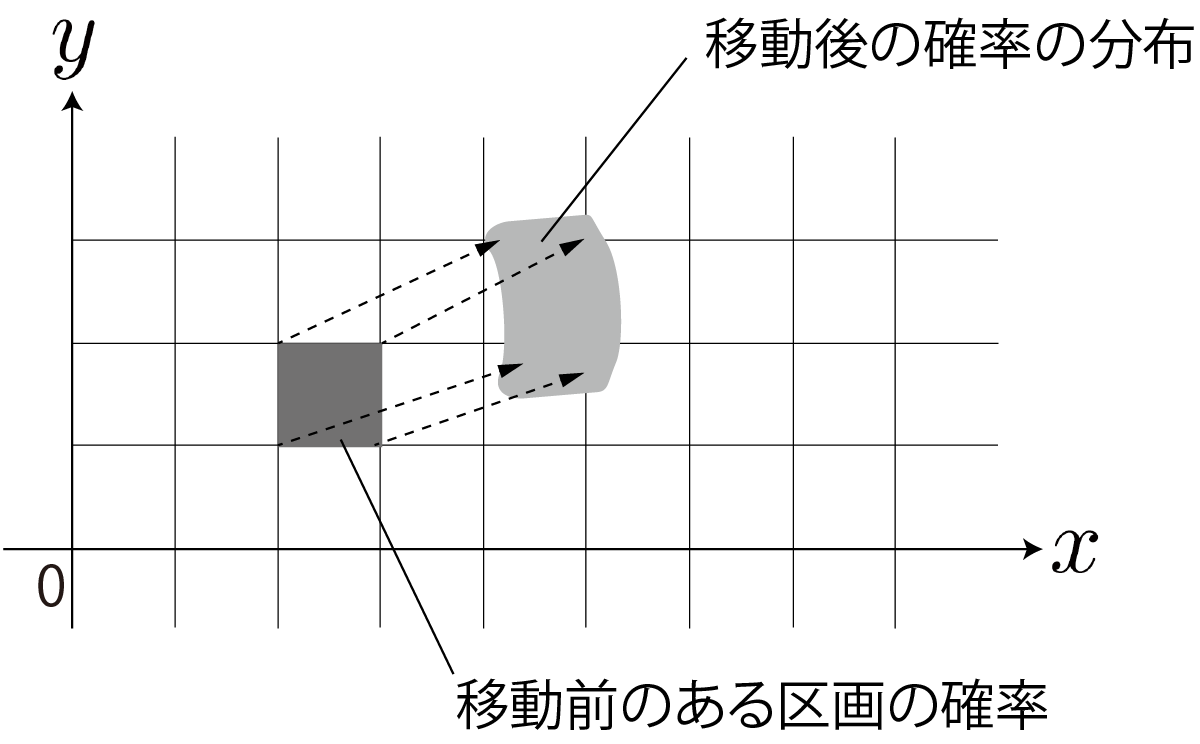
ヒストグラム状の格子を用いた予測

  • 右下図の分布をロボットの動きに合わせて動かす
    • 右図は4章のものの再掲
    • 実際は3次元の格子
  • ロボットが移動したあと、区画にロボットがいる確率:
      • 移動前の格子中の確率から計算される密度
      • 移動後の分布をの中で積分したもの
      • 計算できないモンテカルロ法などの近似
確率ロボティクス第6回

まとめ

  • ロボットの動きの予測
    • 後半（その2）でやったように非線形
    • 線形化か数値計算による近似が必要
  • 今回の内容は「ベイズフィルタ」の一部であり一部の実装
    • センシングを加えると第7回のベイズフィルタに
    • ベイズフィルタの実装
      • 線形化+ガウス分布: （拡張）カルマンフィルタの一部
      • モンテカルロ法: パーティクルフィルタの一部
      • ヒストグラム: ヒストグラムフィルタの一部
確率ロボティクス第6回