実験が足りないような気がするが・・・
- このあと試行を重ねると結果が逆転するかもしれない
- 今回はこの問題について扱う
- 問題へのアプローチ: 完走率の確率分布を推定する
- つまり確率(完走率)自体を確率変数として扱う
- 背景となる考え: 無限回の試行をしないと完走率はそもそも不確か
完走率の確率分布(の予想)
- 完走率(確率変数)を
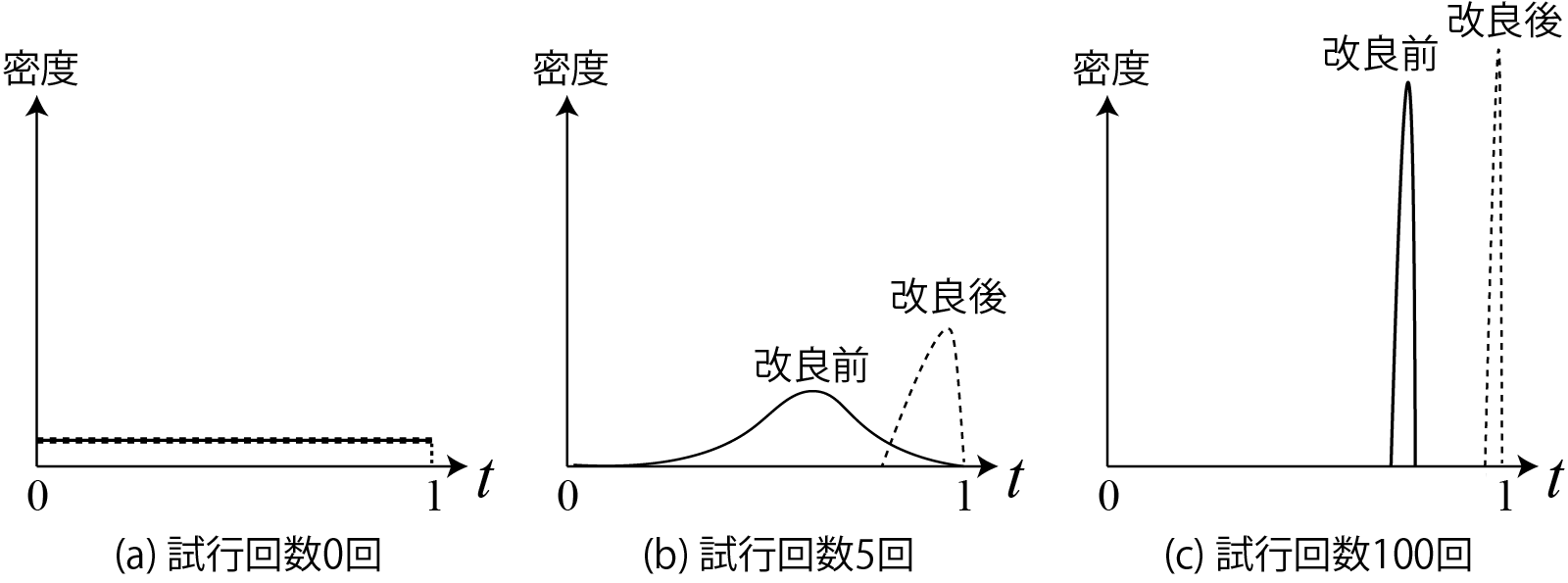
- (a) 試行前: 一様分布に(なにも情報がない)
- (b) 何回か試行: 「完走回数/試行回数」のところにピークが来るが、まだ曖昧
- (c) たくさん試行: 完走率がはっきりして、分布が鋭く

(どうこの分布を計算するかはさておき)
完走率の確率分布を考えると比較ができる
- たくさん試行すると(c)のように改良前後の完走率の分布が(ほぼ)重ならない
- どちらが優れているか(ほぼ)分かる
- 試行が5回ずつ程度だと(b)のように分布が重なっていそう
- 改良前後の完走率が逆転している可能性が無視できないほどある
完走率の確率分布の導出
- 試行結果
- 試行結果
- 上の2式の右辺から
さらに計算
- 教科書は離散化していますが、そのまま計算してみます
- 上記をまとめると
- 前ページの(b)から
- 上の式では定数扱い(
完走率の分布の導出(完了)
- したがって次が成立
- 意味:
正規化すると
- これまでに
完走率の分布の描画
- 改良前のソフトウェアの試行での分布の推移を描いてみましょう
- 完走
- こうなる
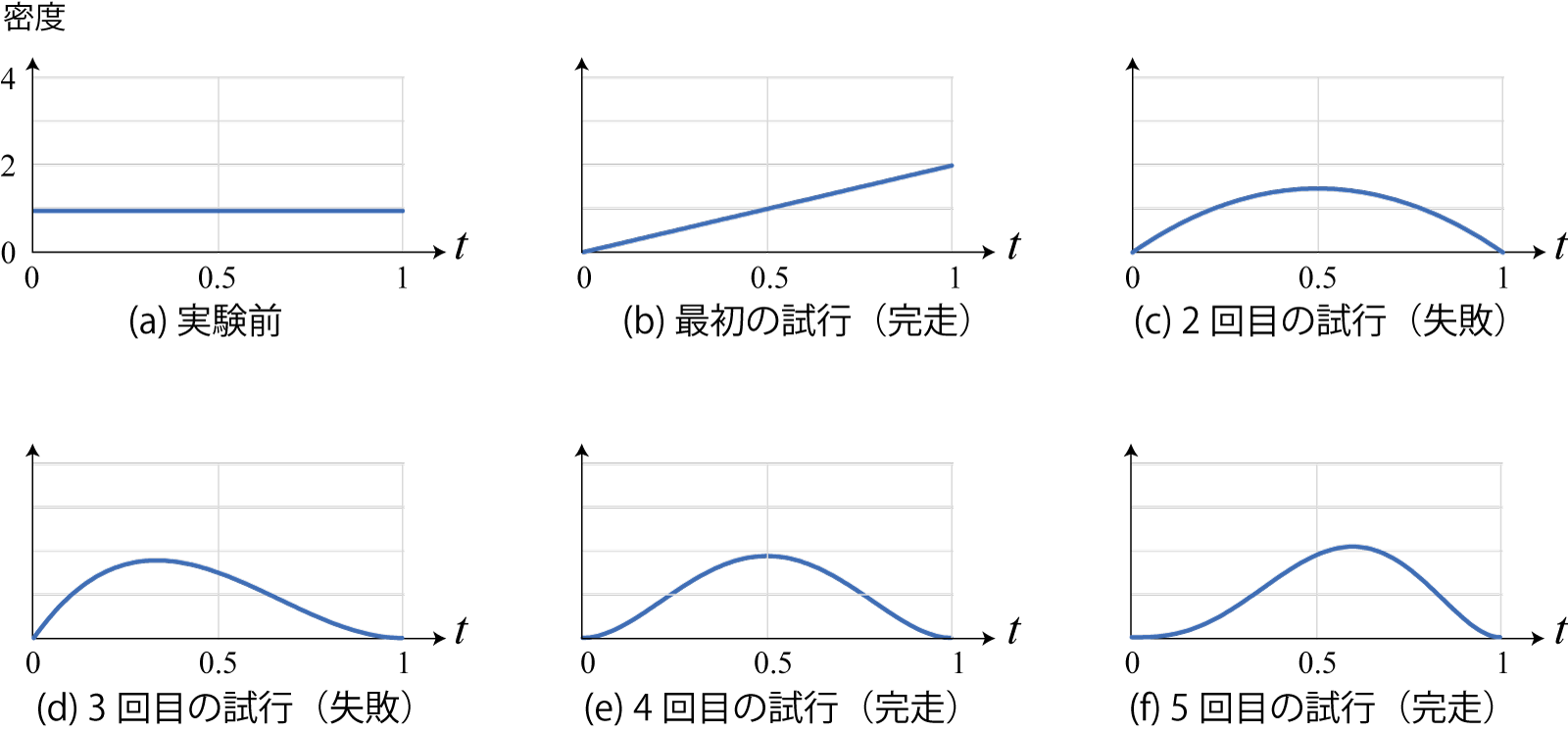
- 完走
分布の比較
- 5回ずつ試行が終わった時点での改良前後での分布の比較
- これも余裕があれば描いてみましょう
- こうなる
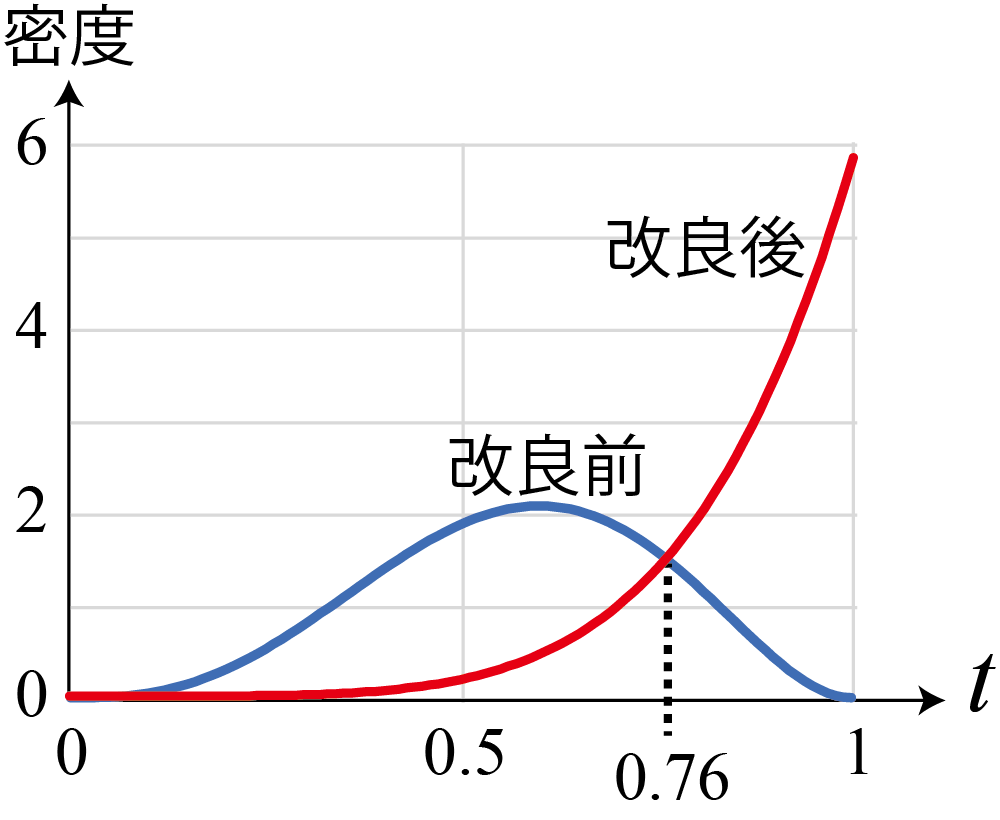
- 改良前の完走率のほうが高い可能性はある
改良前の完走率のほうが高い確率
もし改良後の試行で1回失敗があったら
- 同様に計算すると
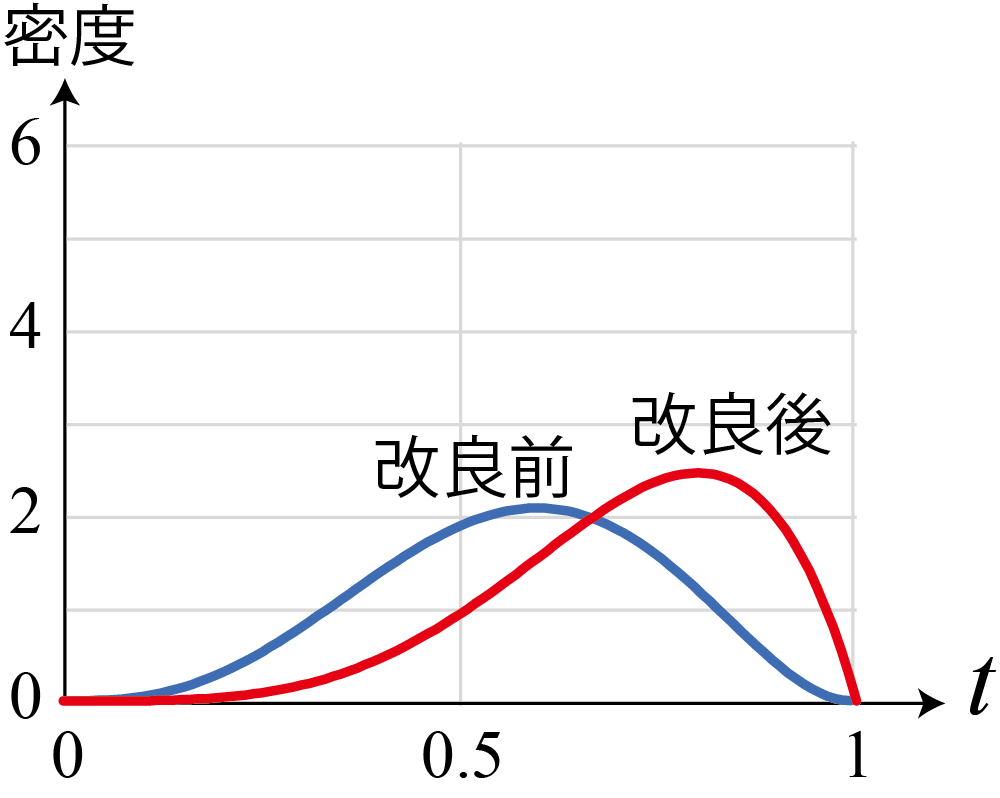
- (試行回数は実験前に決めないといけないので)試行回数は全然足りない
どれくらいの試行回数が必要か?
- 右のグラフ:
- 改良が無意味な確率
- 条件
- 改良前の完走率:
- 改良後の完走率:
- 改良前の完走率:
- 無意味な確率が5%以下になる試行回数
- 100回で10%は下回る
- (学科の学生の感覚よりも)かなり試行回数が必要
ここまでのまとめ
- 試行での比較については、その信頼性が確率の計算で求められる
- 完走率等の確率に対して、さらに確率分布を考える
- どれだけ試行しても、結果が偶然ひっくり返る可能性は0にはならない
- 実験の評価項目、方法を工夫して少ない試行回数で済むように or たくさん試行回数を確保
- 論文指導では「言い切れ」と言われるが、個人的にはかなり疑問
- 他の人に追試してもらうことを前提に、できるだけ有意義な結果や付帯情報の提示を
- 基本、論文の実験結果を鵜呑みにしてはならない
- 自分自身に対しても常に疑いを
ベイズの定理
さっき使ったこの式変形は実はとても重要
- (乗法定理の変形であることはさておき)ベイズの定理と呼ばれる
- ベイズの定理の様々な表記
ベイズの定理の意味
- 新たな情報を分布に反映する式
- 例: 試行
- 例: 試行
- この文脈での用語
尤度・尤度関数
- 尤度:
- 実例:
- 確率変数
実際に観測された
- 確率変数
- 実例:
- 尤度関数:
- 観測された情報
- 実例:
- ベイズの定理には正規化定数があるので、分布でなくても成立
- 観測された情報
周辺尤度
- 意味: 事前分布
- 変形すると(少し)分かる
- (別の情報があれば必ずしも
- 実例(条件付きの分布の場合)
- 変形すると(少し)分かる
- 生物的な意味:
- e.g. 自由エネルギー原理
その他補足
ベータ分布
- 実験の話で求めた事後分布の形
- 一般的な表記
(ベータ関数)
ベルヌーイ試行とベータ分布、共役性
- ベルヌーイ試行: 2値の確率変数で結果が表せる試行
- 完走/失敗、(コインの)表/裏、・・・
- 確率分布は第2回で出てきた「ベルヌーイ分布」
- ベルヌーイ試行の場合(尤度関数がベルヌーイ分布から導出される場合)、
事前分布がベータ分布だと事後分布もベータ分布に- こういう関係を共役性という
- ベルヌーイ分布に対するベータ分布: 共役事前分布と呼ばれる
- 共役性は他の分布のペアにも現れる
- 出てきたときに触れます
- ベイズの定理の計算がパラメータ更新だけで済むのでとても便利
まとめ
- 「必要な実験回数」について考察
- ベイズの定理が自然に出てきた
- ベイズの定理
- ある情報を確率分布に反映するための定理
- (次回以降扱いますが)ロボット工学において重要
- 共役性
- ベイズの定理を解いたり実装したりするときに便利な性質
- なんらかの法則が背景に