分散共分散行列
- 前ページの
- 普通に話す時は「共分散行列」でよい
例: 移動ロボットの実験
- 実験で得られたデータのうち、
- 20試行分のデータ
- 1列目:
- 1列目:
- 計算すべきパラメータ
- データからの共分散の計算方法:
- データからの共分散の計算方法:
計算結果
datamashを使った例
### 平均値 ###
$ cat xy_data.txt | tr ' ' \\t | datamash mean 1 mean 2
3.8822 0.51035
### 分散 ###
$ cat xy_data.txt | tr ' ' \\t | datamash svar 1 svar 2
0.016455957894737 0.19727097631579
### 共分散 ###
$ cat xy_data.txt |tr ' ' \\t | datamash scov 1:2
-0.029138231578947
- これらの値からガウス分布の式を書きましょう
答え
- 式はわかったけど解釈がよくわからない
- グラフを描いてみましょう
2変量ガウス分布の描画
- とりあえず中心からマハラノビス距離
- マハラノビス距離:
- 1次元のものと比較を
- マハラノビス距離:
- 図形は楕円に
- 楕円の式:
- 楕円の式:
とりあえず対角化
- 次のように
- このとき
座標変換
- 前ページ最後の式:
- 次を代入すると
- したがって
- マハラノビス距離が
- マハラノビス距離が
座標を戻す
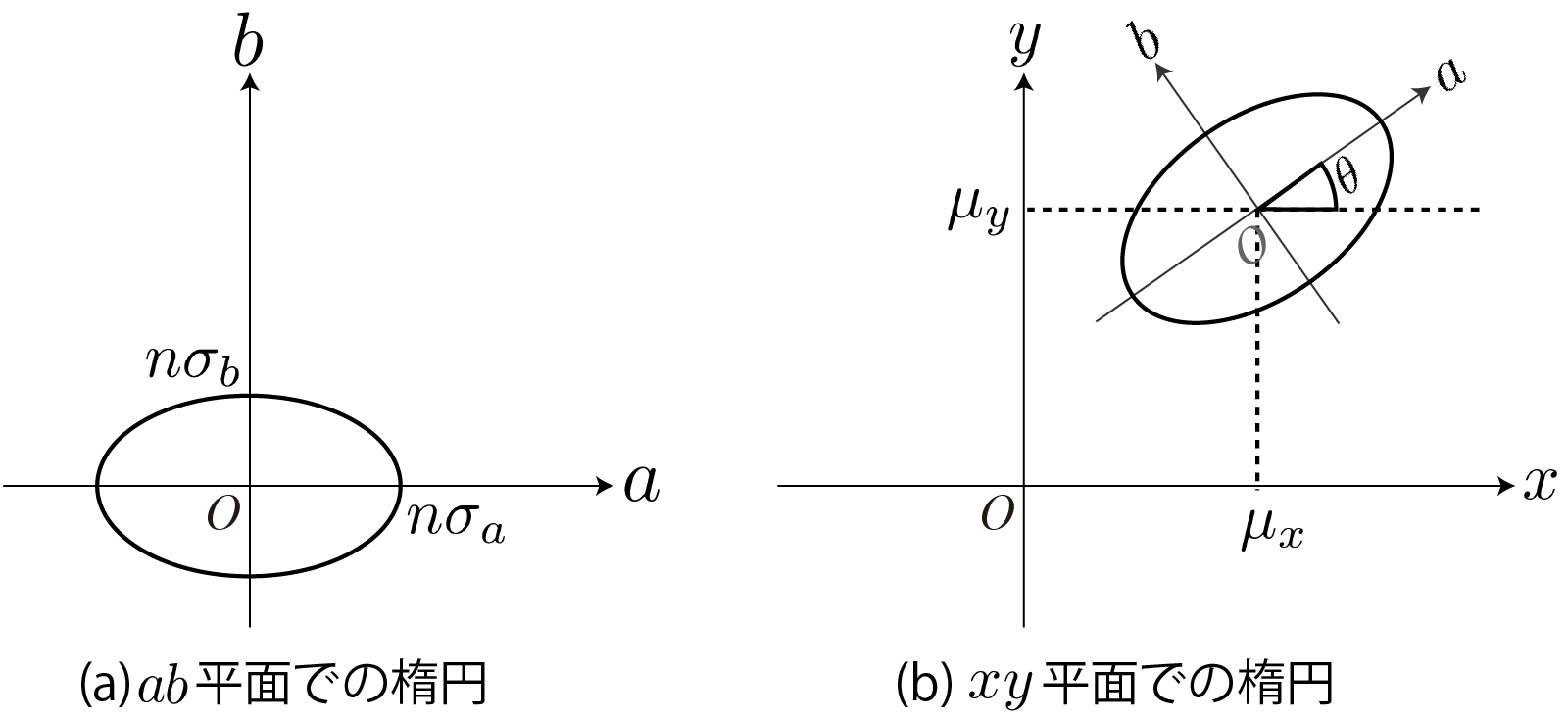
実際の値で描画
- 右図:
- 誤差楕円と呼ばれる
多変量ガウス分布の演算
- 再生性はあるのか
再生性・線形変換
- 例1:
- 答え(1次元のときから類推して書いてみましょう):
- 詳解確率ロボティクスに導出例あり
- 例2:
- 答え(これは次のページで扱います):
- 答え(これは次のページで扱います):
ガウス分布の線形変換
ガウス分布の線形変換(続き)
- 空間が
- 指数部の外にある
- 指数部の括弧内
- 指数部の外にある
多変量ガウス分布の積
- 問題:
- 講義の後半に出てくる形
- 解き方: ひたすら式変形
- 後半のための要望:
多変量ガウス分布の積(解答)
- まず展開
- ここで
- ここで
多変量ガウス分布の積(解答・つづき)
多変量ガウス分布の積(解答・つづき)
- 前ページ最後の行について、次のようにおく
多変量ガウス分布の積(まとめ)
- 問題:
- 答え:
ということでガウス分布になる(どう使うかは講義の後半に期待)
多変量ガウス分布のまとめ
- 多変量ガウス分布(多次元ガウス分布)を導入
- パラメータは平均と分散共分散行列
- 1次元のガウス分布で見た性質を受け継いでいる
- (最近はどんな分野でも)論文に山ほど出てくるので慣れておくとよい
