確率ロボティクス第4回: 連続値と多変量（その2）

千葉工業大学 上田 隆一


This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Creative Commons License

確率ロボティクス第4回（その2）

今回の内容

  • ガウス分布
確率ロボティクス第4回（その2）

ガウス分布

確率ロボティクス第4回（その2）

前半のおさらい

  • 連続的な変数に対して確率密度関数を導入
    • 確率変数が離散でも連続でも分布が表現可能に
  • 次に考えること: 分布が数式で表せないか？
    • 右図のように取得したデータだけで分布を作るのは無理がある
    • 考え方
      • データがなにかの法則にしたがって発生する
      • その法則は数式で表せるかもしれない
        実際に典型的な数式が存在
確率ロボティクス第4回（その2）

ガウス分布（正規分布）の導入

  • 式:
    • : 平均値
    • : 分散
      • 右図の例:
  • 典型的な数式のなかで最も代表的なもの
    • がこまかくばらつく原因が多い場合にこういう形に（中心極限定理）

センサ値や前半にやったロボットの移動距離、向きの誤差は、大きなばらつきの原因がないとガウス分布に従う

確率ロボティクス第4回（その2）

なんで典型的で代表的になるか？

  • 測距センサを例にしましょう
    • 多種多様なばらつき要因: 気温、湿度、振動、外光、回路の電気的な揺らぎ・・・
    • 誤差要因別の誤差を考える
      • 原因が違うので互いに独立と仮定
  • 誤差のない計測値を仮定すると
  • の各値がすべて正になったり、すべて負になったりする確率は低い
    の値はに近いほど高頻度
    • の分布はを中心に釣り鐘型の分布に
確率ロボティクス第4回（その2）

データへの当てはめの例

  • ロボットの移動の例のに対して（単位はdeg）
    • 左図: 20回の試行にガウス分布を当てはめ
    • 右図: さらに試行して100回にして当てはめ

いろいろ考察してみましょう（次ページに例）

確率ロボティクス第4回（その2）

データへの当てはめの例（考察）

  • 20回くらいの試行では分布の形は分からない
    • 100回と比べると形がかなり異なる
  • 当てはめたガウス分布は20回でも100回でも大きな違いはない
    • 20回試行でも平均値と分散はおおかた収束（この場合は）
  • これ以上試行を重ねていくとガウス分布になる？
    • もしかしたら大きな誤差要因がそうさせないかもしれない
      • 2つ以上のガウス分布の重ね合わせになる

確率ロボティクス第4回（その2）

ガウス分布の重ね合わせになる例

  • 詳解確率ロボティクスの、あるセンサ値の分布の例（左図）
    • 日中と日没後でセンサ値の平均値が変わる
    • 他の誤差要因による誤差を圧倒して分布が分離
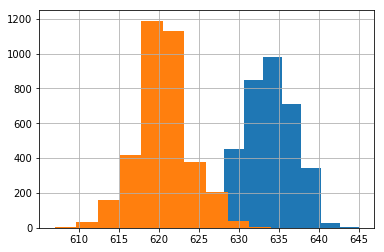
  • 右図
    • オレンジの分布: 昼の14時台の分布を抜き出したもの
    • 青の分布: 朝の6時台の分布を抜き出したもの
確率ロボティクス第4回（その2）

ガウス分布の表記

  • と表記
    • 例: : がガウス分布に従う
  • 変数を明示してと表記することも
確率ロボティクス第4回（その2）

ガウス分布の性質1

  • 問題: それぞれ異なるガウス分布に従う変数（独立）の和の分布は？
    • つまり次のとき、の分布は？
  • 答え:
      • 再びガウス分布に再生性と言われる性質
      • しかも平均値、分散の単純な足し算に

元気な人は証明してみましょう（次ページから証明）

確率ロボティクス第4回（その2）

ガウス分布の性質1（証明）

  • まず分布をで表す



    • 最後の変形: が固定値のの分布: の分布をだけずらしたもの
確率ロボティクス第4回（その2）

ガウス分布の性質1（証明続き）



    • 解き方: 積分を次のように分解
      • 積分内にのガウス分布を残す（積分でになる）
      • 積分の外にの分布を出す（ガウス分布決め撃ちで）
      • 次のスライドに結果だけ示します（計算は教科書で）
確率ロボティクス第4回（その2）

ガウス分布の性質1（証明続き）

    • ここで

確率ロボティクス第4回（その2）

ガウス分布の性質2

  • 問題: がガウス分布にしたがうとき、はどんな分布にしたがうか？
    • どうなる？
  • 答え:
確率ロボティクス第4回（その2）

ガウス分布の性質2（証明）

  • となる確率を考える

  • からを右辺に代入



      • 両辺の積分のなかから
確率ロボティクス第4回（その2）

正規化定数の導入

  • 分布の形と関係ない係数をで表現
    • 例: ガウス分布の形を決めているのは指数部
      （の中）外をで略記することがある

    • は正規化定数と呼ばれる
  • 正規化定数の使われ方
    • 当該部分の詳細に興味がないときに使用
    • 式変形の途中で異なる値になってもで済まさせることがあるので注意
確率ロボティクス第4回（その2）

マハラノビス距離

  • 標準偏差で正規化した距離
    • 値が標準偏差何個分、平均値から離れているかを表す
  • ガウス分布の指数部の値はマハラノビス距離で決まる
確率ロボティクス第4回（その2）

シグマ範囲

  • マハラノビス距離以内の範囲に、データがどれだけ含まれるかを表したもの
    （暗記しておくと便利）
  • ガウス分布の場合、次が成り立つ
    • : 7割弱のデータが収まる
    • : 9割5分のデータが収まる
    • : 1000のうち3つのデータが外れる
  • ついでに
    • 学力偏差値:
確率ロボティクス第4回（その2）

ガウス分布の積

  • 同じ変数に関するふたつのガウス分布、の積を考えてみましょう
    • （深く考えていませんがおそらく）2人の人が別の情報からを推定したので情報を統合したいという状況
    • 下準備で次のようにガウス分布を変形しておく

  • 精度（分散の逆数）を導入
計算は次ページ
確率ロボティクス第4回（その2）

ガウス分布の積（計算）



  • と形を比較

    • と考えると同じ形に
      • ただし上の式は積分してにならないので正規化が必要
確率ロボティクス第4回（その2）

ガウス分布の積（まとめ）

  • ガウス分布同士の積は正規化するとガウス分布に
    • このときできるガウス分布の平均値と精度は
        • 両分布の平均値の重みつき平均。精度の良い方に寄る
        • 精度の単純な和。必ず増加
確率ロボティクス第4回（その2）

ガウス分布のまとめ

  • 変数に様々な種類の雑音ガウス分布に
    • 普遍的
  • 再生性
    • 計算が指数部の計算だけで済む場合が多いプログラムの際に便利
  • 分散、精度の性質
    • 変数の和の分布の場合: 分散の単純和
    • 分布の積の場合: 精度の単純和
確率ロボティクス第4回（その2）