確率ロボティクス第2回（その1）: 確率と信頼性工学

千葉工業大学 上田 隆一


This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License. Creative Commons License

確率ロボティクス第2回（その1）

今回の内容

  • 確率の基礎+信頼性工学
    • 確率を意識しながらロボットを運用する話
  • 内容
    • 確率
    • 簡単な確率の計算
確率ロボティクス第2回（その1）

こんな経験はありませんか？

  • ロボットのなにかの大会に出たロボットが始動しなくてリタイアになった
  • 「運が悪かった」で済ませていませんか？
  • ほんとに運が悪かったんですか？
  • リタイアした原因だけつぶして満足していませんか？
  • なんどもこんなことを繰り返していませんか？
  • そういう人はおそらくロボットへの知識ではなく信頼性工学の知識が足りません
    • 勉強していきましょう
    • 信頼性工学は確率を駆使するので，確率の基礎もおさえていきましょう
確率ロボティクス第2回（その1）

確率

  • 信頼性工学に入る前に
確率ロボティクス第2回（その1）

確率の定義

  • 数学的に厳密なものは難しいので，とりあえずこう考える
    • 何か事象が起こるかどうかを予測するときに，
      同じ状況で統計をとって，起こる割合を確率に
    • 例: ロボットの部品Aが，これまで100回ロボットを起動して
      90回だけ正常に立ち上がった確率と考える
素朴すぎるのですが当面これで議論
確率ロボティクス第2回（その1）

確率の表記

  • 記号での表記: 事象Xの起こる確率をXと表記
    （事象Xはなんでもよい）
    • 前ページの例: Aが正しく立ち上がる
  • あとから出てくるとの違い（本書の場合）
    • この表記の場合はやはそれぞれスカラやベクトル
      • は定義域が数直線やベクトルの空間で厳密に決まった関数
    • 例: サイコロ
      • と書けても 5以外の数 とは書けない
  • XのXは事象なので，なんでも書ける
    • 例: 5以外の数
    • 事象の集合に対する関数になっている
確率ロボティクス第2回（その1）

確率の計算

  • ロボットの起動率の計算を例に
確率ロボティクス第2回（その1）

例題

  • このような単純化されたケースを考えましょう
    • ロボットが10個の部品A, A, , Aで構成されていると仮定
    • ロボットの主電源を入れてしばらくするとAが使えるようになる
      • それぞれ「起動する」と表現
    • Aどれかが起動しないとロボットが正しく起動しない
    • ある部品の起動の成否は他の部品の起動の成否に影響しない
  • 最初の問題
    • Aが正しく起動する確率（起動率）が，他の部品の起動率が
      とした場合，ロボットが正しく起動する確率は？
    • 計算方法は解説していませんが，とりあえずこれまでの知識でどうぞ
確率ロボティクス第2回（その1）

答え

  • Aが起動Aが起動
    と，掛け算になる
    • 答えをみると2回に1回起動しないことが分かる
    • こういう状態で何かに参加しても2回に1回リタイアとなる
  • うんちく
    • 構成要素が1つでも動かないと動かない構成のロボットや機械，
      工場や物流の仕組みのことは，直列システムと呼ばれる
    • 直列システムが正しく稼働する確率:
      • 各構成要素が正しく稼働する確率の掛け算
      • 掛け算で正しく稼働する確率が減る
確率ロボティクス第2回（その1）

もうひとつ問題

  • さっきのロボットを運用しているチームは，部品Aの起動率が低いことを気にして原因を突き止めて起動率をにしました。ロボットの起動率は？
    • 他の部品の起動率はのまま
  • 答え
    • Aが起動（中略）（そんなに改善しない）
    • Aの改善は必要だが他の部品についても改善する必要がある
  • 学生を見ていてよくあるなあと思うやつ
    • 興味のあるところしか見ていなくて全体を見ていない
    • ロボットを走らせると興味のなかったところで不具合が起こり，
      ひどい場合にはそれを棚上げにする毎年リタイア
    • （ロボット関係ないけど）理論派を自称する連中も大抵これ
確率ロボティクス第2回（その1）

さらに問題

  • ロボットの起動率をまで引き上げるには，各部品の起動率をどこまで向上させる必要があるでしょうか？すべての部品を同じ起動率まで引き上げる場合，の値はいくつでしょうか？
  • 答え
  • 「たまに動かないけどまあいいや」みたいな部品は，基本使ってはならない
確率ロボティクス第2回（その1）

ここまでのまとめ

  • 起動率を計算すると，たまに頭で考えていることと違う答えが出てくる
  • 人間は自分の興味に引きずられて現実を歪んだ姿で見る
    • 失敗を冷静に考察できない人はまた同じ失敗をする
    • 確率の計算ができれば，その歪みも多少マシになるでしょう

ということで，もっと確率の計算ができるようにしましょう
確率ロボティクス第2回（その1）

確率の計算

確率ロボティクス第2回（その1）

直列システムの起動率はなぜ掛け算になる？

  • さきほど，直列システムの起動率を掛け算で求めた
    • なんで掛け算？
    • ここでは確率の計算の定理を正しいとして，機械的に考えてみましょう
      • 乗法定理という定理を使う
確率ロボティクス第2回（その1）

乗法定理

  • AとBが起きるAが起きる|Bが起きるBが起きる
    • Aが起きる|Bが起きる: Bが起きることが分かっているときに
      Aが起きる確率（条件付き確率）
      • の右側は「条件」
  • 直列システムに適用するとこうなる
    • Aが起動Aが起動|Aが起動Aが起動
      • Aが起動|Aが起動について考察してみましょう
確率ロボティクス第2回（その1）

独立

  • Aが起動|Aが起動
    • ある部品の起動の成否は他の部品の起動の成否に影響しないと条件にあった
      条件を削除可能
  • このような事象の無関係性を独立という
  • 独立な事象との関係:
      • は集合の共通部分を抽出する演算子
    • 表記:
  • 独立でない場合は従属といわれる
    • 表記:
確率ロボティクス第2回（その1）

直列システムの起動率

  • したがって
    • Aが起動
      Aが起動|Aが起動Aが起動
      Aが起動Aが起動
  • 同様にA，A，・・・を乗法定理で外に出して条件から消していくと
    Aが起動Aが起動
    が成立
確率ロボティクス第2回（その1）

別の例: 冗長化されたシステム

  • 部品Aの起動率を上げるために，次のように複数の部品aに置き換え，
    どれが壊れても問題ないようにしました。aはハブaにつながれています。
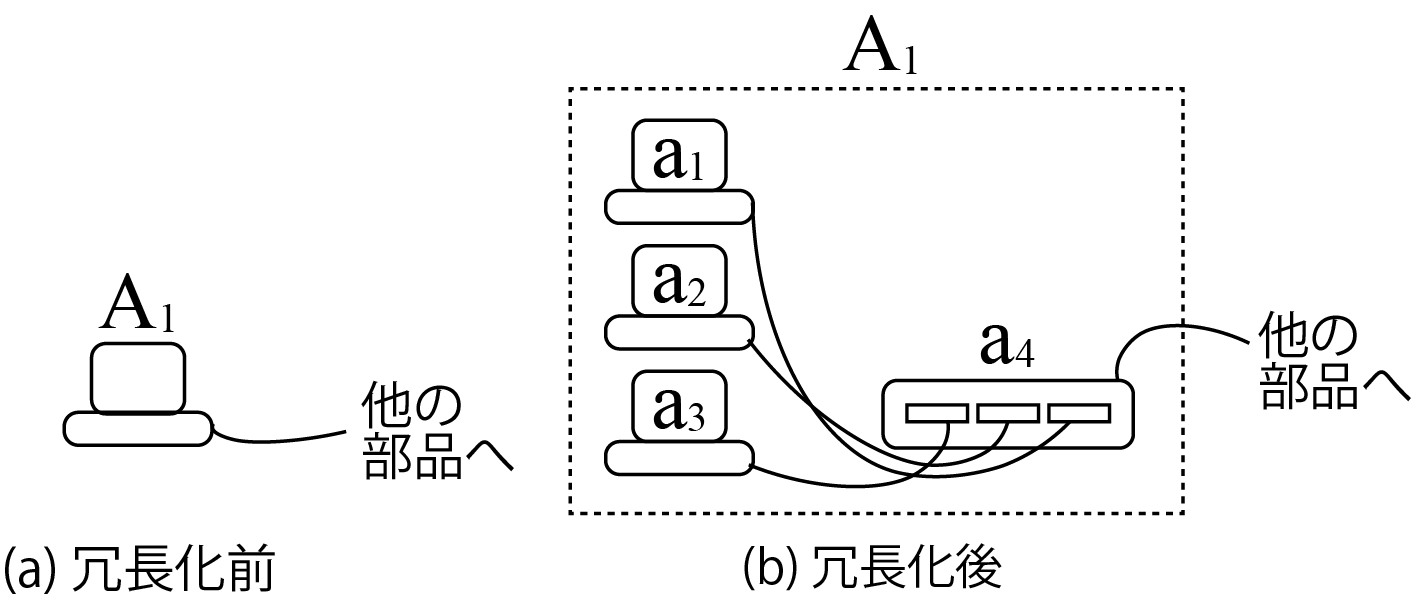
    • 起動率はどう計算するんでしょうか？（こんどは掛け算にはならない）
確率ロボティクス第2回（その1）

加法定理

  • 確率の足し算に関する定理
    • A，Bどちらかor両方起こるAが起こるBが起こる
      AとBが両方起こる
  • とくにAとBが同時に起こりえない場合
    • AあるいはBが起こるAが起こるBが起こる
      が成立
    • AとBが同時に起こりえない: （互いに）排反と表現
      • 例: 「さいころの目が偶数」と「さいころの目が奇数」は排反
      • 排反の場合
        • （あるいは）: 空事象（起こり得ない事象）
確率ロボティクス第2回（その1）

確率の計算方法のまとめ

  • 重要: 実は乗法定理と加法定理しか定理がない
    • 普通の算数よりも規則が少ない
  • 乗法定理
    • XYXYY
    • 独立な場合: XYXY
    • 互いに独立なXに対し: XX
  • 加法定理
    • XYXYXY
      • は左右の集合を合併するときの演算子
    • 排反な場合: XYXY
    • 互いに排反なXに対し: XX
確率ロボティクス第2回（その1）

冗長化したシステムの起動率

  • aの起動率をそれぞれとしましょう
  • aを除いたaが1つ以上起動する確率の計算
    • 「1つ以上起動」を排反な事象に切り分ける
      • aが起動
        • 確率
      • aが起動せず，aが起動
        • 確率:
      • aが両方起動せず，aが起動
        • 確率
    • 合計の確率:
確率ロボティクス第2回（その1）

計算の続き（単一故障点）

  • aが起動しないと冗長化したAは起動しない
    • 単一故障点（単一障害点）と呼ばれる
  • 冗長化したAの計算結果
    • a全体とaは直列なので，前ページの結果に
      aの起動率（とおく）をかける
  • 具体例1:
    • 起動率: （> Aの起動率）
  • 具体例2:
    • 起動率: （< Aの起動率）

結局，aの信頼性が相当高くないと冗長化の効果は少ない

確率ロボティクス第2回（その1）

もうひとつの計算方法: 余事象を使用

  • 余事象
    • ある事象Xに対し，全事象（起こりうる全ての事象）からあるXを除いた事象
    • 事象Xに対して余事象はXと表記
    • サイコロの例: 「偶数が出る」の余事象は「奇数が出る」
  • 余事象を使った計算
    • 「aが1つ以上起動」の余事象は「aが全て起動しない」
    • aが1つ以上起動
確率ロボティクス第2回（その1）

部品が互いに影響を与える場合

  • 今度は次のようなケースを考えてみましょう
    • Aは電源回路で，某チームは
      X君作とY君作の2つのものを使用
      • X君のもの: 高起動率/電流が少し不安定
      • Y君のもの: 低起動率/電流は安定
    • Aの起動率がX君，Y君のAで違う
      （右下の表）
どっちを使ったほうがいい？
確率ロボティクス第2回（その1）

解き方

  • 式をたてる
    • ロボットが起動誰のAか
  • 面倒なので略記
    • AZ
      • 「Aが起動」を単に「A」
      • 誰のAかを単にZ（ZにはX君，Y君どっちかが入る）とする
  • 条件がある場合の乗法定理を使用
      • 条件を無視して乗法定理を使い，最後に条件を入れるだけ
      • 導出は「ロボットの確率・統計」に
確率ロボティクス第2回（その1）

式の展開

  • AZAAAZAZ（部品Aを条件に移動）
    AAZA（不要な条件を消去）
    AAZAZA （Aを条件に移動）
    AAZAZA（独立性から分解）
乗法定理と独立を使って分解していく
（確率ロボティクスや機械学習のアルゴリズムの導出の基本）
確率ロボティクス第2回（その1）

値の代入

  • 最終的な式
    • ロボットが起動Z
      AAZ
      AZA
  • 表の数値を当てはめ
    • Z=X君の場合:
    • Z=Y君の場合:
Y君のものをつかったほうがよい
（どっちもどっちだけど）
確率ロボティクス第2回（その1）

隠れた条件の後付け

  • もうひとつ，アルゴリズムの導出に出てくるタイプの問題を解いてみましょう
  • 問題
    • X君，Y君のチームは，ある期間のロボットの起動率の統計をとっていた
      • ロボットが起動だった
    • ロボットにはX君，Y君のどちらかの電源回路を使っていた
    • X君の電源回路を使った割合は？
  • 補足: X君，Y君の電源回路を使った時のロボットの起動率
    • X君:
    • Y君:
どう解きましょう？
確率ロボティクス第2回（その1）

解法

  • 加法定理の逆をやる
    • ロボットが起動ロボットが起動
      • 「電源回路がX君作」と「電源回路がY君作」は排反で，
        合わせると全事象になるので成立
  • 乗法定理を適用
    • ロボットが起動
      ロボットが起動XXロボットが起動YY
確率ロボティクス第2回（その1）

解法（続き）

  • ここまでに得られている式
    • ロボットが起動
      ロボットが起動XXロボットが起動YY
  • 代入する値の整理
    • 求めたい値（X君の電源回路を使った割合）をとする
      • Y君の割合はとなる
    • X君の電源回路を使ったときのロボットの起動率:
    • Y君の（同上）:
  • 代入
確率ロボティクス第2回（その1）

今の問題のポイント

  • もともと考えていなかった条件をあとから入れることができる
    • ロボットが起動
      ロボットが起動XXロボットが起動YY
      • もともとなかったX，Yが出現
  • 条件が書いてなくても，実はあらゆることが条件になっている
    • ロボットが起動ロボットが起動世の中のあらゆること
    • ロボットの起動と独立な事象を除去すると・・・
      ロボットが起動ロボットの起動に関係するあらゆること
  • FastSLAM[Montemerlo 2003]の導出などで出てくる
確率ロボティクス第2回（その1）

まとめ

  • 確率について入門
    • という記号
    • 乗法定理，加法定理
    • 独立，排反
    • 空事象，全事象，余事象
  • 2つの定理を使った計算
    • 定理はたった2つだが、事象の扱いで頭をひねる必要がある
確率ロボティクス第2回（その1）