機械学習

第9回: 動物におけるクラスタリングの役割と古典的手法

千葉工業大学 上田 隆一

This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

今日やること

• クラスタリングの重要性
• 古典的手法

クラスタリングの重要性

• 第1回のおさらい
  • 右の図は何に見えますか
  • なんで猫に見えるのか？
• たぶん丸い部分1つと三角の部分1つに点をまとめている（クラスタリングしている）
  • 研究例

まとめると何がわかるか

• たとえば目の前になにがあるかを知りたい場合
  • やらなければいけないこと: 視細胞の反応認識対象（猫など）
    • 多数の刺激「猫」という1単語
    • 「減らす」という作業が脳内で必要となる
      • 減らす=代表値（特徴量）にまとめる
• 左図: 実物の畑の作物と、茎と葉を分類した画像
  • ロボット用
  • いろんな色が3色に減っている
  • 人間は右のような分類結果を（時間をかければ）描ける

生物以外でのクラスタリングの役割

• いわゆるビッグデータというやつ
  • 膨大なデータから経営方針を決定
• ロボット
  • 動物と同じ
  • 右図: 掴みやすい面を発見するために、掴める箇所をクラスタリングして一番おおきなクラスタのところをつかむ
    • 動画

クラスタリングの古典的手法

• ロボット分野で30年前から利用されてきたもの
  • k-means法
  • EM法
• 解く問題
  • 点が散らばっているときに、どれとどれが同じグループに属するか決める

k-means法

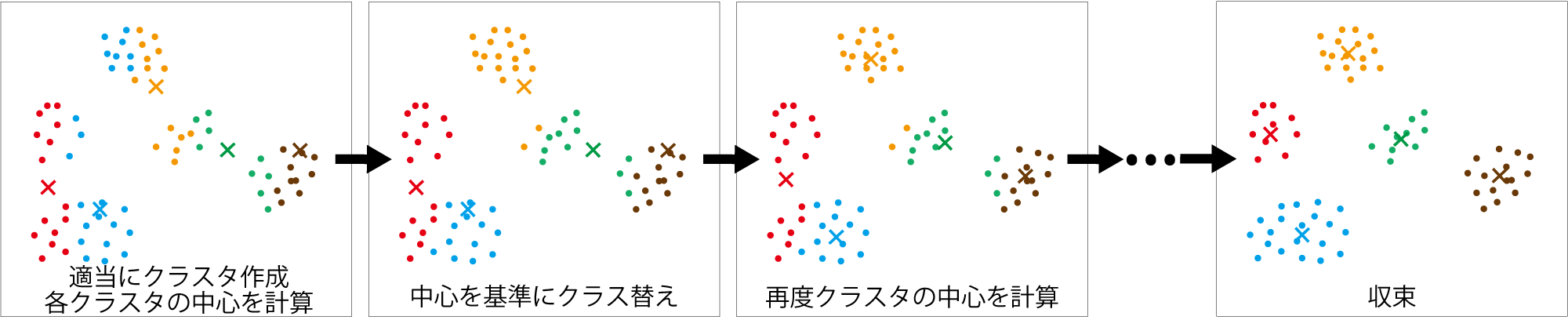
• データを適当にクラスタに分けて、以下の繰り返しで収束させる
  • 各クラスタの中心を求める（図中の印）
  • 各データを最寄りの中心を基準に再度クラスタリング

数字をk-means法でクラスタリングしてみましょう

• 次の9個の数値を3つのクラスタに分けてみましょう
  • (8, 1, 3), (5, 5, 2), (6, 11, 7)
    • かっこは適当に分けた初期のクラス分けを表します
  • 答えは次のページ
• 注意
  • 平均値が同じになったら所属クラスタは適当に選択のこと
  • あるデータに対して近い平均値が2つ以上になったら（同じ距離になったら）
    元いたクラスを替えてみる

こたえ

• 初期値: (8, 1, 3), (5, 5, 2), (6, 11, 7) クラスタの平均値: 4, 4, 8
• 再配置: (1, 5, 2), (3, 5), (8, 6, 11, 7) クラスタの平均値: 2.666..., 4, 8
• 再配置: (1, 2, 3), (5, 5), (8, 6, 11, 7) クラスタの平均値: 2, 5, 8
• 再配置: (1, 2, 3), (5, 5, 6), (8, 7, 11) クラスタの平均値: 2, 5.333..., 8.666...
• 再配置: (1, 2, 3), (5, 5, 6, 7), (8, 11) クラスタの平均値: 2, 5.75, 9.5
• 再配置: (1, 2, 3), (5, 5, 6, 7), (8, 11) （変わらず。終了）

k-means法の問題（考えてみましょう）

• 最初からクラスタ数を決めていいのか?
  • センサやロボットのプログラミングのときに特に困る
    • たとえば画像に人が何人いるかが知りたい。最初から3人と分かることはあまりない。
  • 次回解決
• クラスタがいびつだったら?
  • これはいびつさを解消するようにデータを変換するか、別の方法を用いる（サポートベクターマシーンなど）
• もっと根本的な問題: データの発生した理由を考えていない（つまり場当たり的）

EM法（最尤法）

• EM: expectation maximization
  （どういう意味かはあとで説明）
  
  
• ある確率分布のモデル（数式）を考え、データを
  最ももっともらしく説明するパラメータを求める
  • なんで右図のようなデータが発生したのか?
    データの発生源がいくつかあって、
    そのまわりにデータが発生、と考える

「データの発生源がいくつかあって
そのまわりにデータが発生」

この場合の基本的なモデル: 混合ガウス分布

• 複数のガウス分布を足して、
  正規化（積分して1に）したもの
  • 
    
    • 
      （注意: 円周率ではなく、混合比率）
• 絵に描くと右図のように
  （ちょっと当てはまりは悪いです）

データに対する「一番尤もらしい分布」

• 次の尤度を最大化するものが「一番尤もらしい」と考える
  • • 左辺: データが生成した確率の密度
    • 右辺: 各データの密度の掛け算
    • データは既知なので、最も尤もらしい（最尤な）パラメータや、その尤度を求める問題に
  • 具体的に書くと
    • 左辺
• 対数をとって掛け算を足し算にして、対数尤度を最大化する問題にする
  • • 問題が等価で簡単なものに

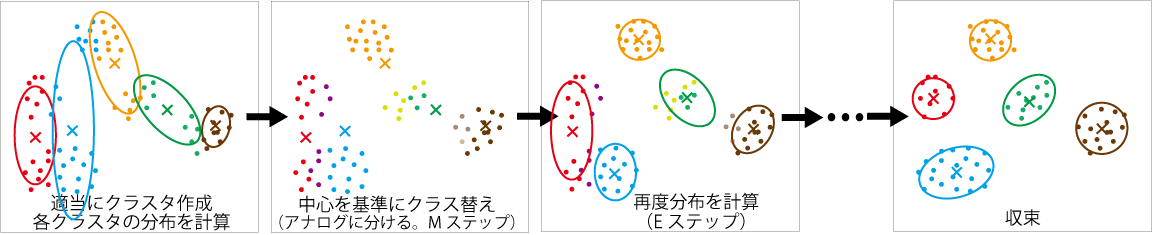
対数尤度が最大になるパラメータの求め方（k-means法と似ている）

1. 最初に適当にクラスタリング
2. Mステップ（maximization step）
   • 尤度が最大となる各クラスタのを算出
3. Eステップ（expectation step）
   • に基づきデータをクラスタリング
     • その時点での各データのクラスタへの所属の確率を計算

Eステップ

• 各データについて、どのクラスタにどれくらいの確率で所属しているのか求めたい
  • 混合ガウス分布のパラメータは固定で
  • k-meansと違って、1つのクラスタへの所属に断定しない
    • 分からないのだから曖昧にしておく
• 数学的には
  • の属するクラスタが番目のクラスタである確率の値を求めたい
    • がの場合すべてに対して
  • のような変数は隠れているので潜在変数と呼ばれる

の計算方法

• は、クラスタのガウス分布の密度に混合比率をかけたものになる
• 計算式の導出
  • （ベイズの定理）
    • : 番目のクラスタのガウス分布
    • : の情報がないときに番目のクラスタにデータがいる確率（）
  • ←計算できる
    • は各クラスタに対するの値の和がになるように決める

Mステップ

• を固定して分布のパラメータを計算
• 方法（で重みをつけて統計をとる）
  • 補助のパラメータを考える
    • 各クラスタの要素の個数に相当
  • 各クラスタの大きさと、平均値、共分散行列をとに基づいて計算

EM法で可能となること/ならないこと

• 可能になること
  • 確率的な考え方の導入
    • （実例がなくて申し訳ないのですが）性能はk-meansより上がる
      • はっきりしないことは曖昧なままにしたほうが変な間違いが少ない
    • 「確率モデルに対して最尤」という基準ができる
    • 他の確率モデルにも適用できる
• 可能にならないこと
  • もっと確率的であってもよい
    • パラメータにも分布がある（混合ガウス分布も確率的にばらつく）
  • ガウス分布の個数が決まっている
    • 不要な個数の分布が消えるまでは性能が高くない

補足資料

EM法の一般的な導出

• p.13の対数尤度、p.14の潜在変数を次のように記述（記号を減らすため）
• を変形
  • 
    （←最後の項は対数尤度）
• 対数尤度を右辺に移動し、各項にをかけてで積分（）
  • 
    
• 左辺の積分はが内にないので外せる

潜在変数を考慮してEM法を導出（続き）

• 右辺に足して0になる2項を増やして配分
  • 
    
    
    
• 新たな関数を定義して整理

できた式

• $ = \mathcal{L}(q, \boldsymbol{\Theta}) + \text{KL}(q || p)$
  • （）: 潜在変数の分布
  • : カルバック・ライブラー距離
    • 分布との形状の違いを数値化したもの
      （一致するとで、違うほどと正の大きな値に）
  • : 変分下界
    • 対数尤度（左辺はこれより値が下にならない。KLが0以上なので）

できた式と使い方

• • （）: 潜在変数の分布
  • : カルバック・ライブラー距離
    • 分布との形状の違いを数値化したもの
      （一致するとで、違うほどと正の大きな値に）
  • : 変分下界
    • 対数尤度（左辺はこれより値が下にならない。KLが0以上なので）
• 使い方
  • をに固定して「良い」を探す（Eステップ）
    • をにするのがよさそうが対数尤度に一致
  • を固定してをに更新（Mステップ）
    • が最大になるように（対数尤度も大きくなってより良い結果に）