前回のおさらい
- 回帰を勉強した
- けど、少ないデータでもひとつにグラフを決めてしまう
- なにが足りないか
- 第6回のようなベイズ的な考えが抜けている
- ベイズ的な考え方をとりいれた回帰がないか?
- ある
ベイズ線形回帰
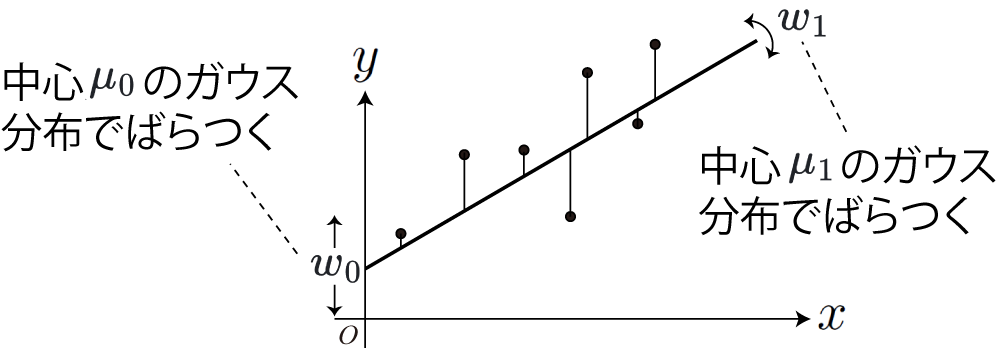
- 関数の分布ってなに?
- 関数の分布ってなに?
- 例:
- 右図:
- どちらも平均値
- データ(丸印)に合うように、ベイズの定理で
- どちらも平均値
ベイズ線形回帰のための数式
ややこしいので意味だけ考えましょう
- 例: 当てはめる式: 多項式
- いくつか仮定を置きましょう
- 仮定1:
- 補足: 分散の逆数
- 仮定1:
回帰のための数式(続き)
- 仮定2:
- 分布
- 分布
回帰のための数式(続き)
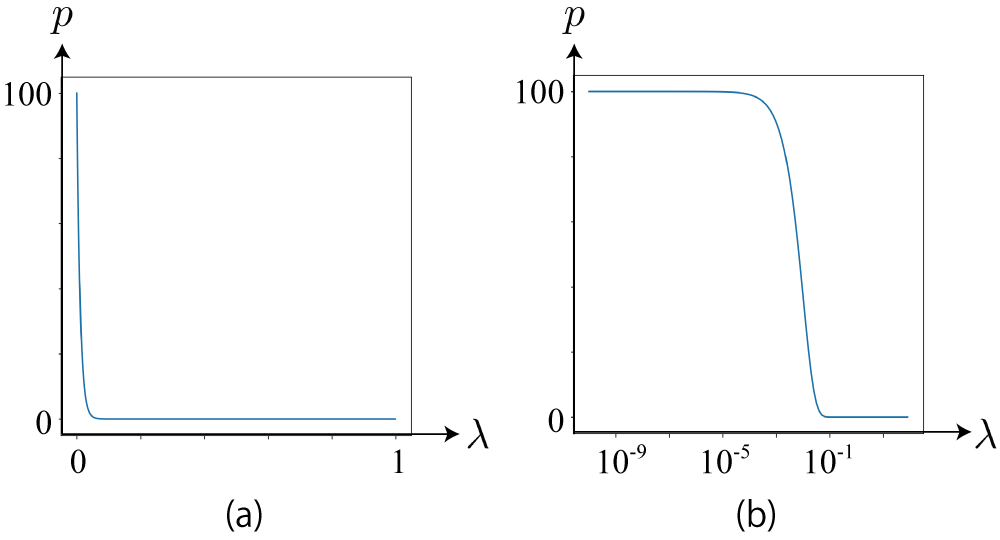
- 仮定3:
- こういう分布:
- 下図(a): ガンマ分布の確率分布
- 下図(b): (a)の横軸をlog尺にしたもの
- こういう分布:
回帰の方法(式だけ見せますね)
(=事前分布のパラメータ)
- 「ガウス-ガンマ分布」と呼ばれる分布
回帰の方法(続き)
- データ
- ベイズの定理を使う
- ベイズの定理を使う
回帰の方法(続き)
-
左辺の事後分布が同じ形だとすると、こういう等式ができる
-
実際に左辺はガウス-ガンマ分布となり、事後分布のパラメータはこうなる
ポイント
- 事前確率と事後確率の分布が同じ形
- 事前確率:
- 事後確率:
- 事前確率:
- 講義だとどうしても原理の話になり、それは重要なのだけど、使うときは前ページの下の4つの式に事前分布のパラメータとデータの値を入力するだけ
- まず大事なことは、使いどころがどこなのかおさえておくこと
データが複数の場合
- 最小二乗法のように一気に計算可能
- データ
- ここで
- ここで
さらに
- いろんな関数に係数をかけて足したもの
- 実は前ページの式がそのまま使える
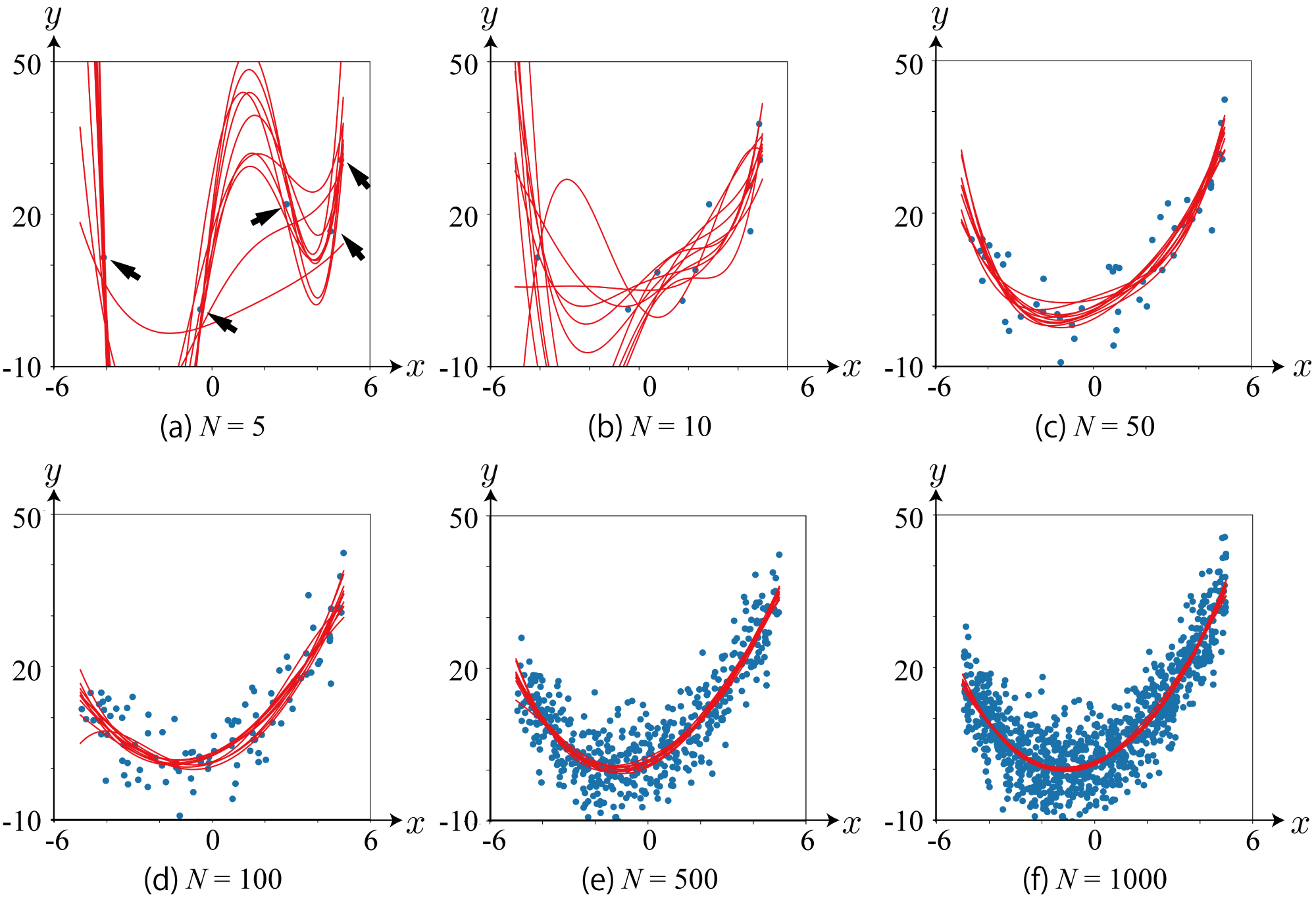
例:
- 少しずつデータを入力して、事後分布から関数(多項式)をサンプリング
- データが増えるにしたがって関数のばらつきが減る
- データ(2次関数からサンプリング)にしたがい、高次のパラメータが
まとめ
- ベイズの定理で回帰がより一般的に
- 関数の分布=パラメータの分布と考える
- データの不足によるあいまいさをも考慮可能に
- ベイズ線形回帰の導出
- 難しいが結果は機械的に使用可能
- 使いどころを間違えなければ誰にでも便利な道具に