機械学習

第6回: 自信のなさの見積もりとベイズ推論

千葉工業大学 上田 隆一


This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

機械学習（と統計）第6回

今日やること

  • 実験結果のベイズ的な考え方
  • 共役
機械学習（と統計）第6回

ベータ分布（再掲）

  • 式:
    • はベータ関数というややこしい関数
  • コインの表、裏がそれぞれ、回出たときに、表が出る確率の分布
    • 投げるほど分布が尖っていく
      • 数学的な解釈: ある確率に収束していく
      • 生物的な解釈: ある確率なのではないかとだんだん確信していく
今日はこれを掘り下げます
機械学習（と統計）第6回

問題

  • 題材: ボールを投げて頭上の籠に入れる玉入れロボットを作りました。これから実験で籠に入る確率を求めます。

  • 最初の問題: まず1回試行したら成功しました。成功率はどれだけでしょうか?
    • 話し合ってみましょう
    • 必要な前提をおいて計算してみましょう
機械学習（と統計）第6回

最初の1回の計算方法

  • まず、成功率をとしましょう
  • 試行前、偏見がなければの分布（確率の密度）はこうなる
    • （注意: 確率がなのではなく、密度がで積分するとになる）
  • ベイズの定理のために尤度を考える
    • 成功、失敗
  • ベイズの定理
    • 成功成功
機械学習（と統計）第6回

最初の1回のポイント

  • 成功したんだから成功率がということはない
  • 最初成功したからといって次に成功するとは限らない
    • ただし、今の時点では次も成功する可能性は高い


グラフがこれらのことを示している
機械学習（と統計）第6回

次の問題

  • 続けて試行したらまた成功しました。確率分布はどうなるでしょうか？
  • 現在の分布:
    • 成功成功
  • 求めたい分布:
    • 成功, 成功
  • 尤度
    • 成功、失敗
機械学習（と統計）第6回

答え

  • ベイズの定理を使う
    • 成功, 成功成功成功
  • グラフから
    • に近い成功率の可能性がより高まる
    • に近い成功率の可能性も残っている
  • 問題: 成功率以下の確率は?
機械学習（と統計）第6回

さらに

  • 3回目、4回目の試行が失敗でした。
    成功率の分布は?
  • 求めたい分布: 成功, 成功, 失敗, 失敗
  • 尤度: 失敗
  • 答え（定数はに吸収）
    • 成功, 成功, 失敗
      失敗成功, 成功
      （上図）
    • 成功, 成功, 失敗, 失敗
      失敗成功, 成功, 失敗
      （下図）
機械学習（と統計）第6回

結局

  • 回成功、回失敗の場合の成功率の分布:
    • 成功回, 失敗回
    • ↑ベータ分布
    • が増えていくとだんだん分布が尖って動かなくなってくる（余裕があれば計算してみましょう）
  • 重要なこと
    • 試行から単純に計算した成功率はだが、「真の」成功率は確定せず、分布となる
    • ある程度実験しないと確からしい成功率は得られない
機械学習（と統計）第6回

ベイズの定理から分かる日常の教訓

（繰り返しになるけど）人間の頭がベイズの定理を厳密に解いているかは分からないが、ベイズの定理を超えて真実を知ることがは原理的に不可能なので・・・

  • 何かが1、2回起こったことで、次どうなるかを決めつけてはいけない
    • 日常的にやってませんか?
  • 試行を重ねると判断が正しくなっていく
    • 年寄りの話しは基本よく聞いたほうがいい
    • が、しかし、頑固になってしまっているので、途中でルールが変わってしまったことに気付かないと年寄りは間違えたことを言うようになる
機械学習（と統計）第6回

ベイズの定理と機械学習

  • いまやった分布の更新は、機械学習の基本的な原理
    • 知識が入るごとに何かの分布が変化して尖っていく
    • 知識が入るまえは平たい分布
  • 確率の確率分布を考える
    • 「成功率」とは確率なので「確率の確率分布」を考えていたことに
      • 混乱しやすいので分からなくなったら頭の整理が必要
機械学習（と統計）第6回

共役

機械学習（と統計）第6回

ベイズの定理の事前・事後確率

  • ベイズの定理の計算は事前確率と事後確率が同じ分布だと簡単
    • ベイズの定理:
    • 前半の例は両方ベータ分布だった
      • 知識が入ったらとの値だけを更新すればよい（すごく簡単）
  • 同じにならないときがある
    • 尤度の形による
機械学習（と統計）第6回

事前・事後確率が同じになる組み合わせ（一部）

の分布（事前・事後分布） の分布（尤度のもとになる分布）
ベータ分布 ベルヌーイ分布
ガウス分布 ガウス-ガンマ分布
多次元ガウス分布 ガウス-ウィシャート分布
ディリクレ分布 多項分布
ガンマ分布 ポアソン分布
  • 分布について
    • ベルヌーイ分布: 前半で扱ったコインの裏表の確率を表す単純な分布
    • 他の分布については各自調査を
  • 現象の性質が自然に上記表に当てはまることもあるが、便宜的に使うこともある
機械学習（と統計）第6回

（続きがありますが）まとめ

  • 確率の確率を考えた
    • 確率や統計値そのものが不確定ということまで考慮しないと、いろいろ議論がおかしなことになる
      • 数回実験しただけで「成功した」と主張するとか
  • 実際のところ、実験での証明には不確かさが残る
    • 「AよりBのほうが1%性能がよい」を
      調べるには膨大な回数の実験が必要
      • 実は研究の世界ではそこまで考えられてなくて、
        p値という謎数値で「証明」とする慣行が残存
  • その計算方法を考えた
    • ベイズの定理が主役
機械学習（と統計）第6回

補足: 様々な分布III

機械学習（と統計）第6回

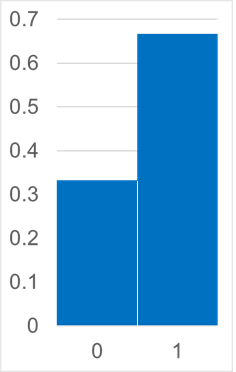
ベルヌーイ分布

名前はいかついが最も単純な分布

  • 確率変数が2値の分布
    • 例: ある重さの偏ったコインがあって、表・裏の出る確率がそれぞれ1/3、2/3
    • 横軸の0: 表、1: 裏
機械学習（と統計）第6回

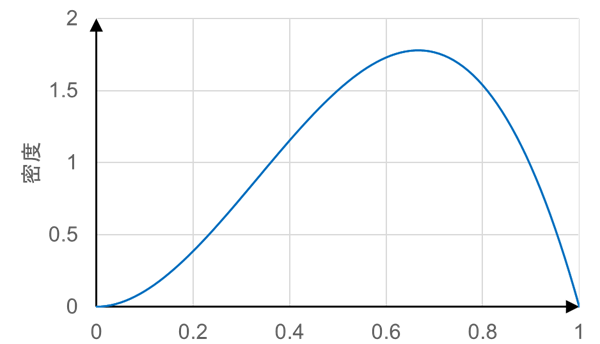
ベルヌーイ分布とベータ分布の関係

  • ベータ分布から確率を選ぶとベルヌーイ分布になる
  • ベルヌーイ分布状の尤度関数を入力するとベータ分布が変形する

機械学習（と統計）第6回

ディリクレ分布

  • ベータ分布を裏表から多値に拡張
    • 多値: ここではさいころの目のように確率変数が3値以上をとるもの
    • さいころの出目の確率の確率
      • ディリクレ分布からさいころが製造されるイメージ
  • 分布の式
      • : とりうる種類の値が出る確率（足すと1）
      • : ベータ分布のに相当
        • だとベータ分布に（導出してみましょう。解答: 次ページ）
  • 図はWikipediaでも見てください
    • ベータ分布を立体化したような形状
機械学習（と統計）第6回

ディリクレ分布からベータ分布への変換

  • なのでこうなる
  • なので、
  • 「と」の分布というのはつまりの分布なので
  • 、、とおくと
機械学習（と統計）第6回