機械学習

第11回: 人工ニューラルネットワークの基礎

千葉工業大学 上田 隆一


This work is licensed under a Creative Commons Attribution-ShareAlike 4.0 International License.

機械学習（と統計）第11回

今日やること

  • 人工ニューラルネットワークってなに？
機械学習（と統計）第11回

人工ニューラルネットワークってなに？

  • まずは問題
    • なんで犬とか猫とか我々は認識できるのか?
      • 脳がやっているということは知っている
      • 脳に神経があることも知っている
    • 脳や神経は具体的にどういう構造なのか?

（https://commons.wikimedia.org/wiki/File:Retina-diagram.svg, by S. R. Y. Cajal and Chrkl, CC-BY-SA 3.0）

機械学習（と統計）第11回

神経細胞

  • 信号を伝える細胞
  • 信号を伝える仕組み
    1. 樹状突起に化学物質をある量受けると電圧が発生
      （発火）
      • 視細胞のように他の刺激で発火するものも
    2. 電圧が軸索を伝って、その先のシナプスから化学物質を放出
    3. 他の細胞が発火
（図: public domain）
機械学習（と統計）第11回

（人工でない）ニューラルネットワーク

  • 脳: 神経細胞が集まって回路を形成
    • 計算をしている（後述）
    • ニューラルネットワークというのはこれのこと
  • 脊髄: 神経が背骨を伝わり体の隅々へ
    • もともと脳ではなくこちらが本体
    • 反射などの計算はここで
  • 末端: 回路の先端が筋肉につながっていてスイッチに
（右図：CC BY-NC-SA 4.0, 脳科学辞典から）
機械学習（と統計）第11回

神経細胞の「計算」

  • スイッチの役割
    • 複数の細胞から信号を受信
    • 信号の総量がある一定値を超えると電圧が発生
    • 電圧: 軸索シナプス
      別の複数の細胞
  • どうやってこんな仕組みで計算できるんでしょう?
    • 身近に似たものはないか?
    • 議論してみましょう
機械学習（と統計）第11回

神経細胞を単純化したモデル

  • 右図のような構造に簡略化（人工ニューロン）
    • 他の個の細胞から信号を受け取る
      • : 他の細胞からの信号の強さ
      • : 信号を受け取った値にかける「重み」
    • ひとつの値だけ信号を出す

      • なら
        • : 閾値（バイアスとも）
      • 接続先は複数だが同じ値を送信
  • 他の細胞も同様にモデル化するともになってディジタル回路に
機械学習（と統計）第11回

人工ニューロンで回路を組んでみる

  • 問題: 2つの数字との符号が同じかどうかを調べる
    • 値が0の場合は正としましょう
    • 答え
機械学習（と統計）第11回

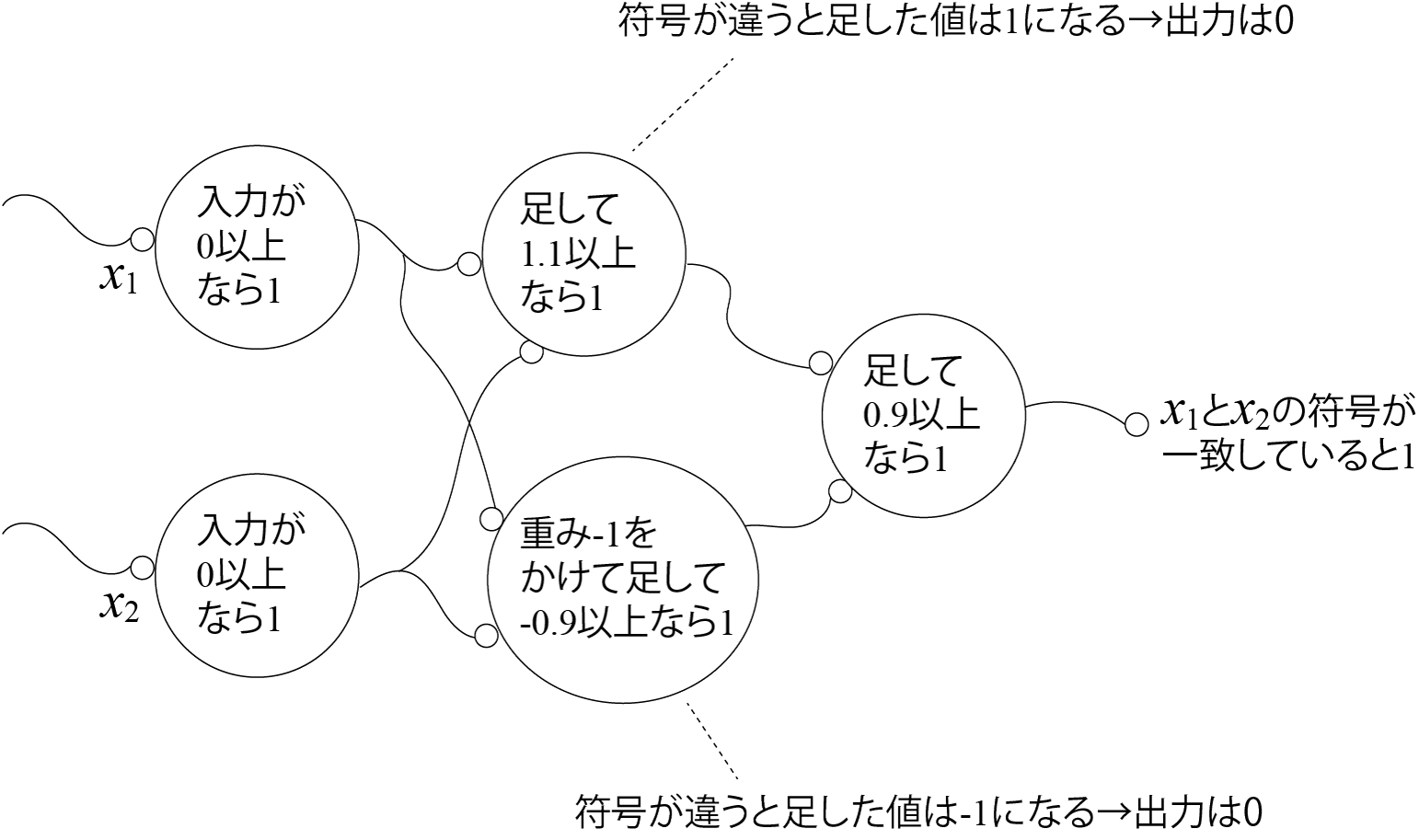
（人工）ニューラルネットワーク

  • 神経細胞は前ページのように組み合わせてプログラムできる
  • 人の脳には860億個の神経細胞
    • 860億個が組み合わさってさまざまな計算をしているのでいろいろできる
      • 目から入った光で猫がいたら「猫！」と叫ぶ（目→脳→口の筋肉）
      • 手を動かして目の前のお菓子をとる（目→脳→腕や手の筋肉）
      • カレーの匂いがしたらよだれが出る（鼻→脳→よだれを出す器官）
      • 講義中にゲームをする（？）
  • コンピュータでも人工ニューロンで計算すれば or 人工ニューロンを実現するようなコンピュータを作れば、脳の計算が可能人工ニューラルネットワーク
機械学習（と統計）第11回

人工ニューラルネットワークの正体

  • やってることは単なる行列の演算
  • 先ほどの例の一番左の「層」
    • 入力: と表現
    • 重み:
      • 上、下のニューロンがそれぞれしか使わないという意味
    • 出力の計算:
      • は閾値:
      • は閾値処理
機械学習（と統計）第11回

あとは繰り返し

  • 1層目（再掲）
    • 入力:
    • 、
  • 2層目
    • 入力（1層目の出力）:
    • 、
  • 3層目
    • 入力（2層目の出力）:
    • 、
機械学習（と統計）第11回

レイヤーでの表現

  • 入出力を線でつなぎ、演算を箱で表現
  • これまで使ってきた例だと1層分が2層に
    • 重みの反映（と閾値の引き算）で1層
      • アフィンレイヤー
    • 閾値処理で1層
      • ステップ関数レイヤー
  • 注意: 右の図ではあまり入出力の数が変わってないが、実際はアフィンレイヤーの前後で変わる
機械学習（と統計）第11回

残った問題: どう学習するか?

  • 動物は生まれたときにある程度プログラミングされた状態だが・・・
    • そのあと成長しても神経細胞は基本的に増えない
    • 猫を識別するにはニューラルネットワークに変更を加えないといけない
    • 頭を開けて配線するわけにはいかない
どうやるの?みなさんは普段どうしてます?（話し合ってみましょう）
機械学習（と統計）第11回

学習の方法: パラメータを変える

  • 例題: ならを出力、そうでなければを出力する人工ニューロン
    • 最初、パラメータはあてずっぽ（右図上）
  • 基本的な方法
    1. 何か入力して出力と正解の「ずれ」を観測する
      • 例えば上のニューロンにを入れるとが出てくる（が出てきてほしいのに）
    2. ずれを小さくするようにパラメータを変える
      • この場合はたとえばとするとに

これを全ニューロンに対してやる（以後はレイヤー表記）

機械学習（と統計）第11回

パラメータをどう変えるか?

  • 案1: 出力を間違えたらあてずっぽで変える
    たくさんパラメータがあると正解は無理
  • 案2: ずれが小さくなるようにパラメータを変える
    • 少しやを変えてもにかにされるので効果が分からない
      • ちょっと変えたらちょっとでもいいので
        誤差が減ってほしい
        （どうすればいいか議論してみましょう）
機械学習（と統計）第11回

対策

  • 方法1: 出力をアナログ値に（次のページ）
  • 方法2: たくさん入力して期待値をとる
    • バッチ、ミニバッチと呼ばれる方法で方法1と共に使われる
機械学習（と統計）第11回

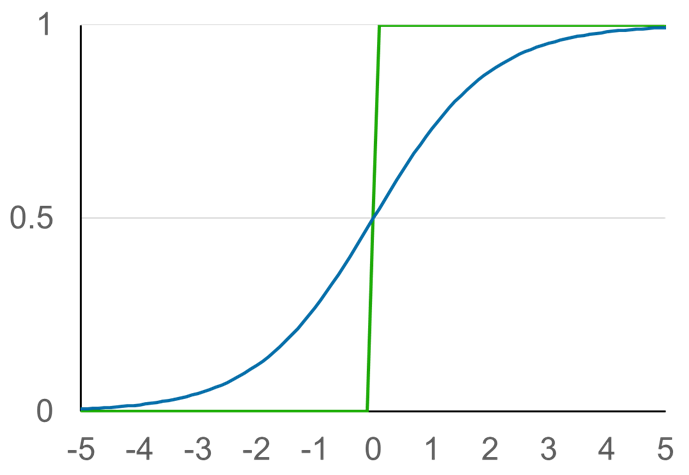
シグモイド関数で微妙にアナログに

  • という関数を使用
  • シグモイド関数のグラフ
    • 青線
    • 緑はこれまでのステップ関数
これでパラメータを少し変えると出力も少し変わるのでずれの修正ができる（メモ: 1, 0でもあとのスライドのように修正ができるので、ここは説明が少し違う。）
機械学習（と統計）第11回

次なる問題: ずれに対してどれだけパラメータを修正するか

  • 誤差逆伝播法
    • 出力側の誤差をどんどん入力側に送っていく
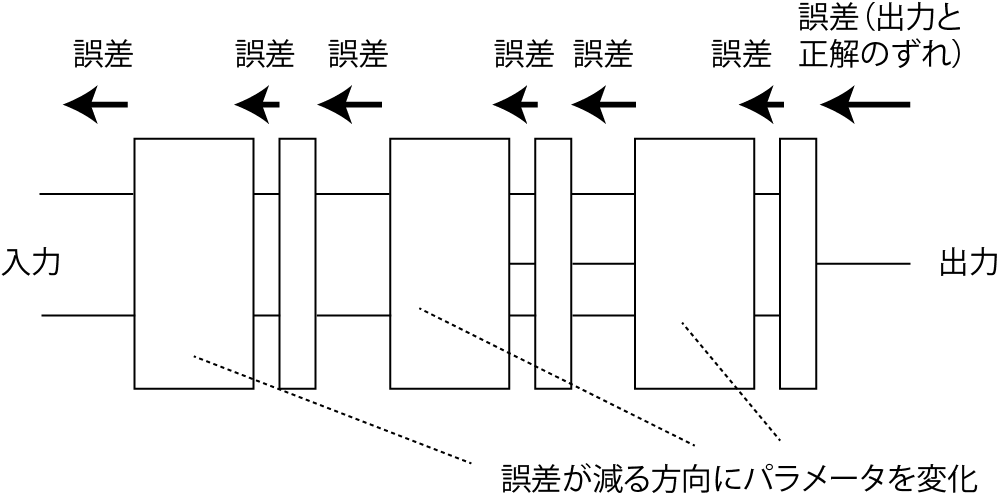
      • 誤差の大きさは、そのニューロン（層）の影響を考えて加減する
    • 送られてきた誤差が小さくなる方向にパラメータを変える
機械学習（と統計）第11回

単純な例

  • 送る誤差の大きさ
    • ある層で誤差が倍になるなら、かけて上流に送る
      • 上の層での値の違いが倍だけ影響するので
    • 右図上: 1入力1出力の単純なレイヤー
      • が入力されてを出力
        誤差が返ってきた
        （出力はもっと小さいべき）
      • なので倍して誤差を送信（を返す）
  • パラメータの修正（計算式の根拠は次ページ）
    • （重みが減る）
    • （閾値が上がる）
機械学習（と統計）第11回

アフィンレイヤーの誤差逆伝播

  • 出力の誤差: と書ける
    • 最終的な誤差に対してが与える影響度
  • 入力（前の層の出力）の誤差: 同様に
      • （行列の計算はさておき）重みの分だけ影響力が増すので、これを上流に送る
  • シグモイドレイヤーも同様に計算すると
    • となる
機械学習（と統計）第11回

アフィンレイヤーのパラメータ修正

  • 誤差に対するパラメータの影響
    • について:
    • について:
  • これらの値をだけ割り引いて元のパラメータから引く
    • 割り引くのはひとつの入力だけでパラメータを大きく変えないため
機械学習（と統計）第11回

問題: p. 14のニューラルネットワークのパラメータ修正

  • ならを出力、そうでなければを出力させたい
    • 右図上の状態から右図下の状態にもっていきたい
  • 修正のための式（p. 19のもの）:
    • 入力値誤差
    • 誤差
  • で（早く収束させるため大きめ）
  • を入力してパラメータを修正してみましょう
機械学習（と統計）第11回

答え

  • 計算（再掲）

    • 入力値誤差
    • 誤差

  • を入力出力、誤差

    • （に近づく）
    • （そのまま）
    • （に近づく）

  • 次にを入力すると？

機械学習（と統計）第11回

答え

  • 計算（再掲）

    • 入力値誤差
    • 誤差

  • を入力出力、誤差

    • はそのまま
    • （に近づく）
      • はから遠ざかる。そういう場合もある。

  • できる人は前方のニューロンに送る誤差も計算を

機械学習（と統計）第11回

まとめ

  • 人工ニューラルネットワーク
    • ニューロンの組み合わせでプログラムできる
    • 誤差逆伝播で学習ができる
  • 次回、次々回で応用を見ていきましょう
機械学習（と統計）第11回